F: Fotometría de la secuencia de una ocultación

En este notebook vamos a analizar (de manera rápida y no muy precisa) los datos obtenidos en la ocultación de una estrella por parte de Tritón (satélite de Neptuno). Partiremos de una serie de FITS que tenemos en la carpeta imagenes/ocultacionTriton/ (son un subconjunto de los datos obtenidos). Si observamos uno de dichos fotogramas veremos algo similar a esto:

[]

import matplotlib.pyplot as plt

import numpy as np
import glob

from astropy.io import fits
from astropy.stats import sigma_clipped_stats

from photutils.detection import DAOStarFinder
from photutils.aperture import aperture_photometry, CircularAperture, CircularAnnulus

Para analizar la secuencia de imágenes vamos a definir una serie de funciones que nos facilitarán estructurar nuestro código y conseguir la curva de luz de la ocultación:

def getImageData(file):
    """
    Abre un fichero fits y devuelve el array de pixeles.
    ----------
    file
        El fichero FITS a abrir
    """

    hdul = fits.open(light)   # Abrimos la imagen
    data = hdul[0].data

    return data

def getMaximumSource(data):
    """
    Obtiene la posición de la fuente más brillante de la imagen. Hemos ajustado los parámetros del algoritmo de detección de fuentes
    para que encuentre a Neptuno, que es la que vamos a usar para alinear las imágenes.
    ----------
    data
        Los datos de la imagen sobre la cual buscar la fuente más brillante.
    """
    mean, median, std = sigma_clipped_stats(data, sigma=3.0)   # Obtenemos datos generales de la imagen

    daofind = DAOStarFinder(fwhm=12.0, threshold=5.*std)       # Encontramos fuentes "gordas" (en nuestro caso queremos localizar Neptuno, en el centro de la imagen
    sources = daofind(data - median)


    # print(sources)

    maxIndex = 0;                                      # Encontramos la fuente más brillante (máximo "flux")
    maxValue = 0;
    for (i, value) in enumerate(sources['flux']):
        if value > maxValue:
            maxValue = value
            maxIndex = i

    sourceMax = np.array([sources['xcentroid'][maxIndex], sources['ycentroid'][maxIndex]])  # Coordenadas de la fuente más brillante

    return sourceMax

def doPhotometry(data, positions):
    """
    Hacemos la fotometría propiamente dicha en las posiciones sobre una imagen y en las coordenadas que nos interesan.
    ----------
    data
        Los datos de la imagen sobre los que hacer la fotometría
    positions
        Coordenadas de las fuentes que queremos analizar
    """
    aperture = CircularAperture(positions, r=3.)       # Mediremos en un círculo de radio 3

    photTable = aperture_photometry(data, aperture)    # Hacemos la fotometría

    res = photTable['aperture_sum'].tolist()           # Devolvemos la suma de cuentas

    return res

def graficasFotometria(cuentasAnalizar, cuentasReferencia):
    """
    Muestra un par de gráficas.
    La primera mostrará los datos de la fuente ocultada y la fuente de referencia.
    La segunda será la curva ajustando los valores con los de la fuente de referencia.
    ----------
    cuentasAnalizar
        Los datos de la fuente a analizar
    cuentasReferencia
        Los datos de la fuente de referencia
    """
    plt.rcParams["figure.figsize"] = (20,10)
    plt.plot(cuentasAnalizar.tolist(), color ="red")
    plt.plot(cuentasReferencia.tolist(), color ="blue")
    plt.show()

    plt.plot((cuentasAnalizar/cuentasReferencia).tolist(), color ="green")
    plt.show()

A continuación programamos nuestra rutina que irá analizando cada imagen, obtenendo la posición de Neptuno para alinear los fotogramas, y ejecutando la fotometría propiamente dicha. Acabaremos con 2 arrays que contendrán las cuentas de la estrella que se oculta y la estrella de referencia.

lights_list = sorted(glob.glob('imagenes/ocultacionTriton/*.fit'))
#lights_list

fuenteAnalizar = np.array([453.44, 326.02])
fuenteReferencia = np.array([153.11, 570.52])

coordInit = (-10, -10)

cuentasAnalizar = np.array([])
cuentasReferencia = np.array([])

numIm = 0

for light in lights_list:
    print(".", end='')        # Imprimimos puntitos
                              #
    if (numIm + 1)%100 == 0:  #
        print("")             #

    if (numIm % 1) == 0:     # Solo vamos a analizar de 10 en 10 (o el número que pongamos)

        data = getImageData(light)                # Obtenemos datos de la imagen

        fuenteMax = getMaximumSource(data)        # Obtenemos la posición de la fuente más brillante (Neptuno en este caso)

        #print(fuenteMax)

        if (coordInit[0] == -10):                 # Si es la primera imagen guardamos sus coordenadas para luego alinear el resto.
            coordInit = np.array(fuenteMax)       #

        desv = coordInit - fuenteMax                     # Calculamos la desviación de la fuente más brillante con respecto a la primera imagen

        nuevaFuenteAnalizar = fuenteAnalizar - desv      # Coordenada de las fuentes que buscamos actualizadas
        nuevaFuenteReferencia = fuenteReferencia - desv  #


        posicionesAnalizar = [nuevaFuenteAnalizar, nuevaFuenteReferencia]

        #print(light)
        #print(posicionesAnalizar)

        phot = doPhotometry(data, posicionesAnalizar)    # Hacemos la fotometría de las dos fuentes

        cuentasAnalizar = np.append(cuentasAnalizar, phot[0])      # Guardamos las fotometrias para graficarlas más tarde
        cuentasReferencia = np.append(cuentasReferencia, phot[1])  #

    numIm += 1

print("")

....................................................................................................
....................................................................................................
...............................

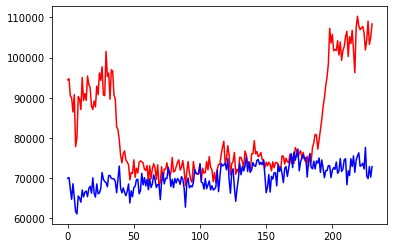
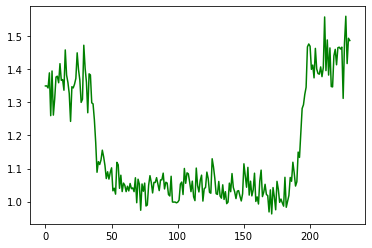
Una vez que tenemos los datos de la secuencia de imágenes podemos graficarlas. En la primera gráfica en rojo tenemos los datos de la estrella ocultada. En azul la estrella de referencia. La ocultación se aprecia perfectamente pero comprobamos que tanto la estrella de referencia como la ocultada tienen un incremento más o menos lineal en su brillo (probablemente por cambios en las condiciones del cielo durante la ocultación). En la última gráfica en verde ajustamos los datos de la ocultación dividiendo por los datos de referencia para corregir dicho problema y los pequeños efectos en cada fotograma.

#print(cuentasAnalizar)
#print(cuentasReferencia)

graficasFotometria(cuentasAnalizar, cuentasReferencia)

curvaLuz = cuentasAnalizar / cuentasReferencia


# Grabamos los datos de la curva de luz
import json

with open('salidas/curvaLuz.json', 'w') as fich:
    fich.write(json.dumps(curvaLuz.tolist()))

---

Ejercicio F.1:

Mejorar la función que calcula la fotometría para restar el fondo utilizando un anillo alrededor de la estrella CircularAnnules. Para ello habrá que calcular el brillo medio de dicho anillo y restarle a las cuentas de la estrella el brillo medio multiplicado por el área de la apertura (aperture.area).

def doPhotometry2(data, positions):
  # Tu código aquí
    return res

---

Ejercicio F.2:

Suavizar la curva de luz obtenida usando una convolución.

# Tu código aquí