B: Ejercicios resueltos del módulo «Introducción a Python»¶
Ejercicio B.1:
Calculemos el valor del polinomio \(f(x) = a x^2 + bx + c\) (con valores \(a\), \(b\) y \(c\)) en un punto \(x\) a su elección.
[1]:
a = 2
b = 1
c = -2
x = 2
resultado = a * x ** 2 + b * x + c
print(resultado)
8
Ejercicio B.2:
Convierta una ascensión recta \(ar = 23.572\) a grados \(^{\circ}\), minutos \('\) y segundos \(''\).
[2]:
ar = 23.572
horas = ar // 1
restoHoras = ar - horas
minutosConDecimales = restoHoras * 60
minutos = minutosConDecimales // 1
restoMinutos = minutosConDecimales - minutos
segundos = restoMinutos * 60
print(f"La Ascensión Recta {ar} son {horas} horas, {minutos} minutos y {segundos} segundos.")
comprobacion = horas + minutos / 60 + segundos / 60**2
print(f"Comprobamos haciendo la operación inversa y sale {comprobacion}")
La Ascensión Recta 23.572 son 23.0 horas, 34.0 minutos y 19.199999999997033 segundos.
Comprobamos haciendo la operación inversa y sale 23.572
Ejercicio B.3:
Hagamos un bloque de código que identifique un grupo de edad para una edad expresada en años según las siguientes tabla:
Menor de 2 años: Bebé
Entre 2 y 11 años: Niño
Entre 11 y 18 años: Adolescente
Entre 18 y 40 años: Adulto joven
Entre 40 y 60 años: Adulto que se cree joven
Entre 60 y 100 años: Viejuno
Más de 100 años: ¿Qué come esta persona?
[3]:
edad = 42 # Cambiar a distintos valores para comprobar nuestro código
if edad < 2:
print("Bebé")
elif edad < 12:
print("Niño")
elif edad < 19:
print("Adolescente")
elif edad < 41:
print("Adulto joven")
elif edad < 61:
print("Adulto que se cree joven")
elif edad < 101:
print("Viejuno")
else:
print("¿Qué come esta persona?")
Adulto que se cree joven
Ejercicio B.4:
Para la lista dada más abajo consigue que quede con los Planetas ordenados (por proximidad al Sol) usando sustituciones, cortes, etc.
[4]:
planetas = ["Mercurio", "Venus", "Plutón", "Tierra", "Júpiter", "Saturno",
"Marte", "Urano", "Neptuno"]
planetas.remove("Plutón") # ¿Qué hace este aquí?
planetas = planetas[0:3] + planetas[5:6] + planetas[3:5] + planetas[6:8]
print(planetas)
['Mercurio', 'Venus', 'Tierra', 'Marte', 'Júpiter', 'Saturno', 'Urano', 'Neptuno']
Ejercicio B.5:
Crear una lista llamada planetas que contenga diccionarios. Cada diccionario debe tener información sobre un planeta (nombre, distancia al Sol (en UAs), y si es terrestre o no. Por ejemplo, planetas[3]['terrestre'] debe dar True y planetas[2]['distanciaSol'] debe dar 1.0.
[5]:
planetas = [
{'nombre': 'Mercurio',
'distanciaSol': 0.39,
'terrestre': True
},
{'nombre': 'Venus',
'distanciaSol': 0.72,
'terrestre': True
},
{'nombre': 'Tierra',
'distanciaSol':1.0,
'terrestre': True
},
{'nombre': 'Marte',
'distanciaSol': 1.52,
'terrestre': True
},
{'nombre': 'Júpiter',
'distanciaSol': 5.2,
'terrestre': False
},
{'nombre': 'Saturno',
'distanciaSol': 9.54,
'terrestre': False
},
{'nombre': 'Urano',
'distanciaSol': 19.19,
'terrestre': False
},
{'nombre': 'Neptuno',
'distanciaSol': 30.06,
'terrestre': False
},
]
print(planetas[3]['terrestre'])
print(planetas[2]['distanciaSol'])
True
1.0
Ejercicio B.6:
Dada una distancia en UAs imprimir el nombre del planeta cuya órbita está más cerca. Necesitamos el ejercicio B.5 resuelto.
[6]:
distancia = 3.76
distanciaAOrbita = 10000000
planetaMasCercano = None
for planeta in planetas:
if distancia > planeta['distanciaSol']: # Esto es un poco chapuzas, lo arreglaremos luego
d = distancia - planeta['distanciaSol']
else :
d = planeta['distanciaSol'] - distancia
if d < distanciaAOrbita:
distanciaAOrbita = d
planetaMasCercano = planeta
print(planetaMasCercano['nombre'])
Júpiter
Ejercicio B.7:
En el ejercicio B.1 calculamos el valor de una función polinómica de grado 2. Construyamos una función llamada polinomio que admita como parametros x, a, b y c y devuelva el resultado de la evaluación del polinomio.
[7]:
def polinomio(x, a, b, c):
return a * x**2 + b * x + c
polinomio(2, 2, 1, -2)
[7]:
8
Ejercicio B.8:
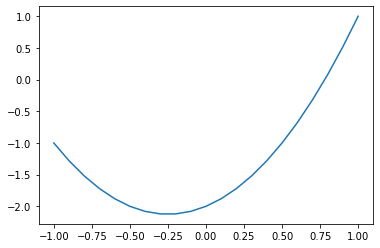
Hagamos una función evaluaPolinomio usando la función polinomio del ejercicio anterior devuelva una lista de tuplas \((x, f(x))\) evaluando el polinomio en diferentes \(x\). Como parámetros debe admitir xMin, xMax, xStep (incremento de evaluación entre xMin y xMax), a, b y c. Luego prueba las última líneas comentadas… ¡a ver que pasa!
Nota: Para que funcione la última parte del ejercicio (que grafica el resultado) hace falta instalar un paquete de Python llamado matplotlib. Para hacerlo abrimos un nuevo Anaconda prompt, activamos el entorno cursoAstronomia y ejecutamos:
> conda install -c conda-forge matplotlib
Es posible que tengamos que reiniciar el Kernel de JupiterLab para que tenga efecto la instalación del nuevo paquete: Kernel \(\rightarrow\) Restart Kernel....
[8]:
def evaluaPolinomio(xMin, xMax, xStep, a, b, c):
x = xMin
puntos = [] # Lista vacia
while x < xMax:
puntos.append( (x, polinomio(x, a, b, c)) )
x = x + xStep
return puntos
puntos = evaluaPolinomio(-1, 1, .1, 2, 1, -2)
import matplotlib.pyplot as plt # Esto aún no hay que entenderlo. Lo veremos más adelante.
x, y = zip(*puntos)
plt.plot(x, y)
plt.show()
Ejercicio B.9:
Hagamos una función similar a la del ejercicio B.7 llamada polinomioN, pero que acepte un argumento x con valor por defecto 0.0 y un número indeterminado de argumentos que serían los coeficientes a, b, c del polinomio de grado igual al número de coeficientes menos uno (si te pasan 3 parámetros será un polinomio de grado 2).
[9]:
def polinomioN(*coef, x = 0.0):
coeficienteActual = len(coef) - 1
res = 0
for c in coef:
res = res + c * x ** coeficienteActual
coeficienteActual = coeficienteActual - 1
return res
print(polinomioN(3, 2, 1, -2, x=2.0))
32.0
Ejercicio B.10:
Creemos una función evaluaF similar a la del ejercicio B.8 que evalue en varios puntos (de xMin a xMax en pasos de xStep). Pasaremos como parámetro una nueva función raizCubica y sierra que viene definida por \(sierra(x) = x \pmod 1\).
[10]:
def raizCubica(x):
return x**(1.0/3.0)
def sierra(x):
return x%1
def evaluaF(func, xMin = 0, xMax = 4.0, xStep = 0.01):
x = xMin
puntos = []
while x < xMax:
puntos.append( (x, func(x)) )
x = x + xStep
return puntos
puntos1 = evaluaF(raizCubica)
puntos2 = evaluaF(sierra)
import matplotlib.pyplot as plt
x, y = zip(*puntos1)
plt.plot(x, y)
x, y = zip(*puntos2)
plt.plot(x, y)
plt.show()

Ejercicio B.11:
Si quisieramos listar todos los números primos menores de un valor n utilizar la función anteriormente definida esPrimo() para cada valor posible sería bastante ineficiente. Vamos a implementar una función que haga la criba de Eratóstenes que devuelva una lista de todos los primos menores de n.
[11]:
n = 20000
def esPrimo(numero):
for n in range(2, numero):
if (numero % n == 0):
return False
return True
def getPrimosMenores(n):
primos = []
for i in range(2, n):
if (esPrimo(i)):
primos.append(i)
return primos
def cribaEratostenes(n):
posiblesPrimos = [True for x in range(n)] # Inicializamos una tabla con n "True". Esta tbla marcará i un numero es primo
i = 2
while i*i <= n:
if posiblesPrimos[i]: # Si el numero por el que vamos es primo
for h in range(i*2, n, i): # Recorremos los multiplos de este numero por encima
posiblesPrimos[h] = False # Y los vamos tachando
i = i + 1
primos = []
for i in range(2, n):
if posiblesPrimos[i]:
primos.append(i)
return primos
import time
t1 = time.perf_counter()
primos = getPrimosMenores(n)
t2 = time.perf_counter()
print(f"Obtener los primos menores que {n} con la función esPrimo ha llevado {t2-t1} segundos.")
#print(primos)
t1 = time.perf_counter()
primos = cribaEratostenes(n)
t2 = time.perf_counter()
print(f"Obtener los primos menores que {n} con la criba de Eratóstenes ha llevado {t2-t1} segundos.")
#print(primos)
Obtener los primos menores que 20000 con la función esPrimo ha llevado 0.7798599090001517 segundos.
Obtener los primos menores que 20000 con la criba de Eratóstenes ha llevado 0.002030547000686056 segundos.
Ejercicio B.12:
Creemos una clase llamada Polinomio que nos permita encapsular la información de un polinomio de grado arbitrario n. Dicha clase debe almacenar la información de sus coeficientes y debe proveer métodos para:
obtener los coeficientes del polinomio,
para obtener el coeficiente con índice
n,para obtener el grado del polinomio,
para evaluar el polinomio en cualquier punto
xypara obtener una lista de puntos evaluados similar a la del ejercicio B.8.
[12]:
class Polinomio:
coeficientes = []
def __init__(self, *coeficientes):
self.coeficientes = coeficientes
def getCoeficiente(self, grado):
return self.coeficientes[self.getGrado()-grado]
def getGrado(self):
return len(self.coeficientes) - 1
def evalua(self, x):
coeficienteActual = self.getGrado()
res = 0
for c in self.coeficientes:
res = res + c * x ** coeficienteActual
coeficienteActual = coeficienteActual - 1
return res
def evaluaF(self, xMin = -2, xMax = 2, xStep = 0.01):
x = xMin
puntos = []
while x < xMax:
puntos.append( (x, self.evalua(x)) )
x = x + xStep
return puntos
pol1 = Polinomio(1.25, 2, -1, -2)
print(f"Los coeficientes del polinomio: {pol1.coeficientes}")
print(f"El coeficiente de grado 2 es: {pol1.getCoeficiente(2)}")
print(f"El grado del polinomio es: {pol1.getGrado()}")
print(f"El polinomio en x=2.0 vale: {pol1.evalua(2.0)}")
puntos1 = pol1.evaluaF()
pol2 = Polinomio(2, 0, 0)
puntos2 = pol2.evaluaF()
import matplotlib.pyplot as plt
x, y = zip(*puntos1)
plt.plot(x, y)
x, y = zip(*puntos2)
plt.plot(x, y)
plt.show()
Los coeficientes del polinomio: (1.25, 2, -1, -2)
El coeficiente de grado 2 es: 2
El grado del polinomio es: 3
El polinomio en x=2.0 vale: 14.0
