F: Integración de imagenes en color¶
Las imágenes RGB/SHO se pueden producir utilizando la capacidad de matplotlib para crear imágenes de tres colores. En general, una imagen RGB es una matriz $ N:nbsphinx-math:times `M :nbsphinx-math:times 3` $, donde \(N\) es la dimensión \(x\) y \(M\) es la dimensión \(y\).
El 3 representa que hay tres canales, el rojo, el verde y el azul, respectivamente. Se puede especificar una cuarta capa que representa el valor alfa (\(\alpha\)-channel) o transparencia (no confundir con las imágenes en filtro \(ha\)). Se puede consultar algo más sobre espacios de color en la Wikipedia.
Las imágenes a color por una cámara normalmente vienen a partir de una matriz de fotosensores (para cada píxel) con filtros de distinto color formando una matriz o mosaico de Bayer.
Matplotlib tiene varias herramientas para manipular imágenes en color en matplotlib.colors.
Las herramientas de visualización de Astropy se pueden utilizar para estirar la imagen y escalar las capas individuales (R, G y B) de la imagen RGB. Cada capa debe estar en una escala de 0.0 a 1.0 para floats (o de 0 a 255 para números enteros). Los valores que see encuentren fuera de este rango serán recortados.
Lupton et al. (2004) describe un algoritmo «óptimo» para producir imágenes compuestas por los canales RGB a partir de tres matrices independientes. Este método se implementa como una funcion de astropy a traves de make_lupton_rgb.
Además haremos uso de algunas funciones de la biblioteca OpenCV (una biblioteca de visión por computadora), que debemos instalar. Ojo, la instalación tardará un buen rato y tendrá que descargar muchos paquetes:
> conda install -c conda-forge opencv
Imagen virtual¶
Creamos una imagen virtual de 100x100 pixeles con valores aleatorios para los tres canales RGB.
Aplicamos la funcion `make_lupton_rgb <https://docs.astropy.org/en/stable/api/astropy.visualization.make_lupton_rgb.html>`__ para obtener la imagen RGB.
[1]:
import numpy as np
import matplotlib.pyplot as plt
from astropy.visualization import make_lupton_rgb
[2]:
plt.figure(figsize=(10, 10))
image_r = np.random.random((100,100))
image_g = np.random.random((100,100))
image_b = np.random.random((100,100))
image = make_lupton_rgb(image_r, image_g, image_b, stretch=0.5)
plt.imshow(image, origin = 'lower')
[2]:
<matplotlib.image.AxesImage at 0x7f1be787bf70>
Estructura interna de la imagen en color¶
Una imagen en color, a diferencia de una imagen monocroma, tiene 3 canales y, por lo tanto, tiene 3 valores asociados a esos canales.
[3]:
image
[3]:
array([[[142, 65, 15],
[217, 2, 27],
[ 67, 134, 131],
...,
[107, 24, 154],
[ 57, 143, 132],
[159, 94, 45]],
[[153, 30, 110],
[125, 83, 123],
[103, 59, 151],
...,
[ 82, 157, 75],
[131, 141, 26],
[ 13, 53, 153]],
[[ 0, 133, 123],
[141, 137, 31],
[108, 96, 128],
...,
[ 63, 92, 106],
[195, 35, 46],
[ 58, 94, 104]],
...,
[[ 19, 145, 59],
[ 67, 127, 115],
[110, 23, 82],
...,
[ 74, 51, 106],
[ 15, 159, 107],
[ 82, 42, 155]],
[[121, 118, 100],
[192, 91, 5],
[ 71, 89, 150],
...,
[106, 24, 84],
[100, 90, 133],
[ 44, 6, 195]],
[[ 97, 102, 117],
[111, 132, 17],
[ 65, 2, 152],
...,
[ 31, 173, 98],
[136, 77, 71],
[ 39, 131, 63]]], dtype=uint8)
Para comprobar que valores hay en un canal concreto debo de buscar en la matriz los pixeles que quiero y luego el canal normalmente ordenado en RGB (0 - rojo, 1 - verde, 2- azul):
[4]:
image[0:10, 0:10, 0] # [pixel_inicial_y:pixel_final_y, pixel_inicial_x: pixel_final_x, canal]
#canal rojo
[4]:
array([[142, 217, 67, 129, 114, 164, 44, 20, 112, 69],
[153, 125, 103, 121, 90, 128, 167, 65, 115, 145],
[ 0, 141, 108, 100, 99, 41, 24, 68, 124, 124],
[ 41, 82, 29, 128, 35, 109, 25, 136, 90, 124],
[ 52, 158, 11, 102, 161, 138, 122, 175, 9, 7],
[149, 165, 206, 129, 111, 67, 87, 27, 136, 86],
[ 46, 105, 117, 40, 91, 133, 77, 85, 137, 56],
[ 94, 67, 98, 78, 54, 36, 152, 116, 162, 56],
[139, 148, 44, 52, 113, 135, 3, 115, 40, 169],
[136, 99, 7, 189, 96, 100, 81, 150, 169, 143]], dtype=uint8)
[5]:
image[0:10, 0:10, 1] #canal verde
[5]:
array([[ 65, 2, 134, 149, 116, 24, 53, 174, 165, 145],
[ 30, 83, 59, 127, 24, 90, 25, 75, 112, 99],
[133, 137, 96, 106, 135, 141, 144, 151, 72, 136],
[138, 69, 138, 57, 150, 114, 34, 13, 133, 88],
[128, 10, 218, 91, 111, 149, 137, 3, 86, 129],
[ 41, 116, 49, 127, 20, 131, 181, 124, 147, 115],
[151, 9, 78, 159, 156, 96, 13, 90, 90, 81],
[144, 131, 61, 86, 128, 104, 145, 128, 32, 5],
[129, 40, 106, 117, 169, 69, 132, 147, 127, 77],
[139, 140, 156, 29, 155, 60, 51, 111, 59, 143]], dtype=uint8)
[6]:
image[0:10, 0:10, 2] #canal azul
[6]:
array([[ 15, 27, 131, 42, 88, 74, 132, 78, 34, 44],
[110, 123, 151, 25, 131, 61, 100, 159, 110, 55],
[123, 31, 128, 132, 100, 126, 126, 26, 70, 26],
[142, 112, 139, 133, 93, 73, 126, 102, 118, 60],
[124, 144, 37, 37, 7, 30, 70, 124, 149, 109],
[ 71, 28, 0, 90, 172, 96, 11, 99, 26, 126],
[ 9, 162, 61, 83, 34, 100, 157, 148, 71, 140],
[ 91, 77, 156, 156, 144, 138, 17, 84, 85, 190],
[ 66, 97, 17, 77, 22, 118, 145, 51, 132, 46],
[ 58, 85, 148, 54, 48, 157, 145, 26, 52, 48]], dtype=uint8)
Podemos cambiar los valores de un canal concreto a partir de cualquier operacion matemática:
[7]:
canal = 1 # Canal que quiero cambiar. En nuestro caso hemos seleccionando el canal verde
len_y, len_x, color = np.shape(image) # Averiguando las dimensiones de mi imagen
image[:,:,canal] = image[:,:,canal]/1.5 # voy subiendo en y hasta completar toda la imagen
[8]:
plt.figure(figsize=(10, 10))
plt.imshow(image, origin = 'lower')
[8]:
<matplotlib.image.AxesImage at 0x7f1bdf56eb20>
Ejemplos con imágenes reales¶
Grupo Hickson 88, SDSS¶
[9]:
import matplotlib.pyplot as plt
from astropy.visualization import make_lupton_rgb
from astropy.io import fits
from astropy.utils.data import get_pkg_data_filename
# Lee las tres imágenes descargadas desde aquí:
g_name = get_pkg_data_filename('visualization/reprojected_sdss_g.fits.bz2')
r_name = get_pkg_data_filename('visualization/reprojected_sdss_r.fits.bz2')
i_name = get_pkg_data_filename('visualization/reprojected_sdss_i.fits.bz2')
g = fits.open(g_name)[0].data
r = fits.open(r_name)[0].data
i = fits.open(i_name)[0].data
plt.figure(figsize=(10, 10))
rgb_default = make_lupton_rgb(i, r, g, filename="salidas/ngc6976-default.jpg")
plt.imshow(rgb_default, origin='lower')
plt.show()

[10]:
plt.figure(figsize=(10, 10))
rgb = make_lupton_rgb(i, r, g, Q=12, stretch=0.2, filename="salidas/ngc6976.jpeg")
plt.imshow(rgb, origin='lower')
plt.show()

Pilares de la creación, Hubble¶
[11]:
import numpy as np
import matplotlib.pyplot as plt
from astropy.io import fits
from astropy.visualization import make_lupton_rgb
forc=np.float_()
r=fits.open("imagenes/eagle/673nmos.fits")[0].data
g=fits.open("imagenes/eagle/656nmos.fits")[0].data
b=fits.open("imagenes/eagle/502nmos.fits")[0].data
[12]:
plt.figure(figsize=(10, 10))
rgb_default = make_lupton_rgb(r,g,b,Q=1,stretch=100,filename="salidas/pilar.jpg")
plt.imshow(r, origin='lower')
plt.show()

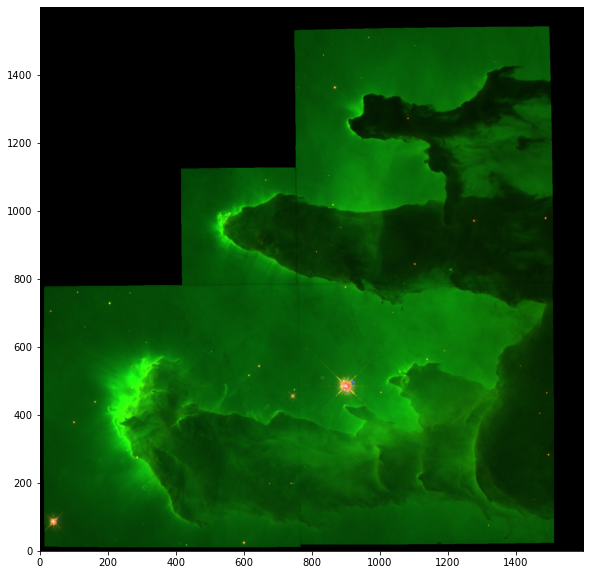
[13]:
plt.figure(figsize=(10, 10))
rgb_default = make_lupton_rgb(r,g,b,Q=0.001,stretch=300,filename="salidas/pilar.jpg")
plt.imshow(rgb_default, origin='lower')
plt.show()
[14]:
plt.figure(figsize=(10, 10))
rgb_default = make_lupton_rgb(r,g*0.1,b,Q=0.001,stretch=50,filename="salidas/pilar.jpg")
plt.imshow(rgb_default, origin='lower')
plt.show()

[15]:
plt.figure(figsize=(10, 10))
rgb_default = make_lupton_rgb(r*0.8,g*0.1,b,Q=0.001,stretch=50,filename="salidas/pilar.jpg")
plt.imshow(rgb_default, origin='lower')
plt.show()

Nebulosa de la Tarantula, SAG¶
[16]:
import numpy as np
import matplotlib.pyplot as plt
from astropy.io import fits
from astropy.visualization import make_lupton_rgb
from registrar import registra_lista, imprimir_info
from rotar import rotar_imagen
from trasladar import shift_image, desplazar_imagen
import cv2
r = fits.open("imagenes/salidaCalibracion/sho/imagenFinal_Sii.fit")[0].data
g = fits.open("imagenes/salidaCalibracion/sho/imagenFinal_H-alpha.fit")[0].data
g_header = fits.open("imagenes/salidaCalibracion/sho/imagenFinal_H-alpha.fit")[0].header
b = fits.open("imagenes/salidaCalibracion/sho/imagenFinal_Oiii.fit")[0].data
Tenemos que intentar alinear las imágenes para que las estrellas de cada canal coincidan. Como veremos las funciones rotar_imagen y despazar_imagen no funcionan como deberian.
[17]:
rgb = [r, g, b]
rgb_rotado = rotar_imagen(rgb)
reg_desplazado = desplazar_imagen(rgb_rotado)
La imagen 1 está rotada -213 grados
La imagen 2 está rotada -28 grados
La imagen 1 se ha desplazado en (x, y) = (-222, -3738)
La imagen 2 se ha desplazado en (x, y) = (-88, -4387)
Tampoco parece funcionar la librería de astroalign
[18]:
import astroalign as aa
registered_image, footprint = aa.register(r, g)#, fill_value=None, max_control_points=50, detection_sigma=5, min_area=5)
---------------------------------------------------------------------------
MaxIterError Traceback (most recent call last)
Cell In[18], line 2
1 import astroalign as aa
----> 2 registered_image, footprint = aa.register(r, g)#, fill_value=None, max_control_points=50, detection_sigma=5, min_area=5)
File ~/anaconda3/envs/cursoAstronomia2/lib/python3.8/site-packages/astroalign.py:488, in register(source, target, fill_value, propagate_mask, max_control_points, detection_sigma, min_area)
454 def register(
455 source,
456 target,
(...)
461 min_area=5,
462 ):
463 """Transform ``source`` to coincide pixel to pixel with ``target``.
464
465 Args:
(...)
486
487 """
--> 488 t, __ = find_transform(
489 source=source,
490 target=target,
491 max_control_points=max_control_points,
492 detection_sigma=detection_sigma,
493 min_area=min_area,
494 )
495 aligned_image, footprint = apply_transform(
496 t, source, target, fill_value, propagate_mask
497 )
498 return aligned_image, footprint
File ~/anaconda3/envs/cursoAstronomia2/lib/python3.8/site-packages/astroalign.py:361, in find_transform(source, target, max_control_points, detection_sigma, min_area)
359 inlier_ind = _np.arange(len(matches)) # All of the indices
360 else:
--> 361 best_t, inlier_ind = _ransac(
362 matches, inv_model, PIXEL_TOL, min_matches
363 )
364 triangle_inliers = matches[inlier_ind]
365 d1, d2, d3 = triangle_inliers.shape
File ~/anaconda3/envs/cursoAstronomia2/lib/python3.8/site-packages/astroalign.py:594, in _ransac(data, model, thresh, min_matches)
591 break
593 if good_fit is None:
--> 594 raise MaxIterError(
595 "List of matching triangles exhausted before an acceptable "
596 "transformation was found"
597 )
599 better_fit = good_fit
600 for i in range(3):
MaxIterError: List of matching triangles exhausted before an acceptable transformation was found
No obstante probamos a generar una imagen en falso color a través de los canales H-alpha SII y OIII creando una paleta SHO.
[19]:
rgb_default = make_lupton_rgb(r, g, b,Q=1,stretch=3000,filename="salidas/shoTarantula.jpg")
#rgb_default = make_lupton_rgb(r, g, b, Q=0.001, stretch=1000,filename="salidas/shoTarantula.jpg")
[20]:
plt.figure(figsize=(8, 8))
plt.imshow(rgb_default, origin='lower')
plt.show()

[21]:
from astropy.visualization import simple_norm
from astropy.visualization import (MinMaxInterval, LogStretch, ImageNormalize)
# Create interval object
interval = MinMaxInterval()
vmin, vmax = interval.get_limits(rgb_default)
# Create an ImageNormalize object using a SqrtStretch object
norm = ImageNormalize(vmin=vmin, vmax=vmax, stretch=LogStretch())
plt.figure(figsize=(8, 8))
plt.imshow(rgb_default, origin='lower', norm=norm)
plt.show()

Podemos comprobar que las estrellas de los diferentes canales no han coincidido unas con otras. Mas tarde corregiremos este problema.
[22]:
plt.figure(figsize=(8, 8))
plt.imshow(rgb_default[2000:2500,2000:2500], origin='lower', norm=norm)
plt.show()

Image denoise¶
Al igual que la reduccion de ruido se puede aplicar antes de generar la imagen RGB, también podemos reducir ruido después de generar dicha imagen aunque no es conveniente eliminar mucho ruido después del estirado que se genera al realizar la imagen en color.
Para la reducción de ruido usaremos el método `fastNlMeansDenoisingColored <https://docs.opencv.org/3.4/d1/d79/group__photo__denoise.html>`__ de la biblioteca OpenCV
[23]:
import numpy as np
import cv2
from matplotlib import pyplot as plt
dst = cv2.fastNlMeansDenoisingColored(rgb_default,None,10,10,7,21)
Para normalizar la imagen y estirarla mejor podemos usar MinMaxInterval que determina los límites de los valores en función de los valores mínimo y máximo de la matriz de la imagen.
Los límites se pueden determinar llamando al método .get_limits() que toma la matriz de valores.
Por último creamos el objeto ImageNormalize que pasaremos a matplotlib
[24]:
interval = MinMaxInterval()
vmin, vmax = interval.get_limits(dst)
# Create an ImageNormalize object using a SqrtStretch object
norm = ImageNormalize(vmin=vmin, vmax=vmax, stretch=LogStretch())
plt.figure(figsize=(8, 8))
plt.imshow(dst, origin='lower', norm=norm)
plt.show()

Guardamos la imagen generada
[25]:
SHO = fits.PrimaryHDU(data=dst.astype(np.float32), header = g_header)
SHO.writeto("salidas/salidaCalibracion/SHO.fit", overwrite=True)
Localización de una imagen a traves de WCS¶
World Coordinate Systems (WCS) describen las transformaciones geométricas entre un conjunto de coordenadas y otro. Una aplicación común es mapear los píxeles de una imagen en la esfera celeste. Otra aplicación común es mapear los píxeles a la longitud de onda en un espectro.
astropy.wcs (documentación) contiene utilidades para gestionar las transformaciones del World Coordinate Systems (WCS) definidas en varias convenciones estándar FITS. Estas transformaciones funcionan tanto del píxel en la imagen a coordenadas como de coordenadas hacia el píxel en la imagen.
Para ello usaremos la función WCS de la biblioteca de astropy. A esta función debemos pasar la cabezera de la imagen que queramos sacar las coordenadas. ¡Atención! El programa de captura deberá haber anotado dicha información en la captura para poder obtener las coordenadas de la imagen. Si no, haría falta un paso previo de resolución de placas.
[26]:
from astropy.wcs import WCS
from astropy.io import fits
h_header = fits.open("salidas/salidaCalibracion/sho/imagenFinal_H-alpha.fit")[0].header
SHO = fits.open("salidas/salidaCalibracion/SHO.fit")[0].data
wcs = WCS(h_header)
wcs
WARNING: FITSFixedWarning: RADECSYS= 'FK5 ' / Equatorial coordinate system
the RADECSYS keyword is deprecated, use RADESYSa. [astropy.wcs.wcs]
WARNING: FITSFixedWarning: 'datfix' made the change 'Set MJD-OBS to 58887.129340 from DATE-OBS'. [astropy.wcs.wcs]
[26]:
WCS Keywords
Number of WCS axes: 2
CTYPE : 'RA---TAN' 'DEC--TAN'
CRVAL : 84.3359148996 -69.3257259717
CRPIX : 2048.0 2048.0
CD1_1 CD1_2 : -3.38076526016e-06 -0.00026594291957
CD2_1 CD2_2 : 0.000265979746215 -3.38029717098e-06
NAXIS : 4096 4096
Aquí nos aparece cierta informacion, la mas relevante es: + CRVAL: RA y Dec del pixel central. + CRPIX: valor del pixel central. + CD1: separacion entre un pixel y otro en RA. + CD2: separacion entre un pixel y otro en Dec.
Un ejemplo del uso de WCS es pixel_to_world para convertir coordenadas de píxel a coordenadas RA y Dec:
[27]:
coordenadas = wcs.pixel_to_world(30, 40)
coordenadas
[27]:
<SkyCoord (FK5: equinox=2000.0): (ra, dec) in deg
(85.90508779, -69.84845846)>
Del mismo modo podemos usar world_to_pixel para obtener coordenadas RA y Dec a través coordenadas de píxel en mi imagen:
[28]:
x_pixel, y_pixel = wcs.world_to_pixel(coordenadas)
x_pixel, y_pixel
[28]:
(array(30.), array(40.))
Si intentamos buscar unas coordenadas RA y Dec fuera de mi campo imagen voy a obtener un NaN:
[29]:
from astropy.coordinates import SkyCoord
import astropy.units as u
coords = ["1:12:43.2 +31:12:43"] #ra y dec
c = SkyCoord(coords, unit=(u.hourangle, u.deg))
c
[29]:
<SkyCoord (ICRS): (ra, dec) in deg
[(18.18, 31.21194444)]>
[30]:
x_pixel, y_pixel = wcs.world_to_pixel(c)
x_pixel, y_pixel
[30]:
(array([nan]), array([nan]))
Generando una rejilla (grill) de RA y Dec¶
Podemos utilizar el WCS para definir proyecciones en Matplotlib.
[31]:
fig = plt.figure(figsize=(8, 8))
ax = fig.add_subplot(1, 1, 1, projection=wcs)
im = ax.imshow(dst, norm=norm, origin='lower')
ax.coords[0].set_ticklabel_position('l')
ax.coords[0].grid(color='white', ls='dotted')
ax.set_ylabel('RA')
ax.coords[1].set_ticklabel_position('b')
ax.coords[1].grid(color='white', ls='dotted')
ax.set_xlabel('Dec');
plt.savefig('salidas/grild_ra_dec.jpg')

Regiones¶
Ademas del manejo de las líneas de la cuadrícula, la clase WCSAxes se comporta como una instancia normal de Matplotlib Axes, y los métodos como imshow(), plot(), scatter(), etc., funcionarán y trazarán los datos en coordenadas de píxeles por defecto.
En el siguiente ejemplo trazaremos los marcadores y el rectángulo en coordenadas de píxeles:
[32]:
fig = plt.figure(figsize=(8, 8))
ax = fig.add_subplot(1, 1, 1, projection=wcs)
im = ax.imshow(dst, norm=norm, origin='lower')
# La siguiente línea hace que el nivel de zoom ya no cambie,
# de lo contrario Matplotlib tiene tendencia a alejar el zoom cuando se añaden superposiciones.
ax.set_autoscale_on(False)
# Añadir un rectángulo con la esquina inferior izquierda en la posición de píxel (3000, 3000) con una
# anchura y altura de 100 y 100 píxeles respectivamente.
from matplotlib.patches import Rectangle
r = Rectangle((2500., 1500.), 500., 500., edgecolor='yellow', facecolor='none')
ax.add_patch(r)
# Añade tres marcadores en (40, 30), (100, 130) y (130, 60).
#El color de la cara es un blanco transparente (0,5 es el valor alfa).
ax.scatter([2000, 0, 4000], [2000, 2000, 2000], s=100, edgecolor='white', facecolor=(1, 1, 1, 0.5))
ax.coords[0].set_ticklabel_position('l')
#ax.coords[0].grid(color='white', ls='dotted')
ax.set_ylabel('RA')
ax.coords[1].set_ticklabel_position('b')
#ax.coords[1].grid(color='white', ls='dotted')
ax.set_xlabel('Dec');

Podemos identificar regiones que queramos destacar de nuestra imagen
[33]:
fig = plt.figure(figsize=(8, 8))
ax = fig.add_subplot(1, 1, 1, projection=wcs)
im = ax.imshow(dst, norm=norm, origin='lower')
# La siguiente línea hace que el nivel de zoom ya no cambie,
# de lo contrario Matplotlib tiene tendencia a alejar el zoom cuando se añaden superposiciones.
ax.set_autoscale_on(False)
#Para el caso especial en el que el WCS representa coordenadas celestes, se pueden pasar otras entradas a get_transform(). Estas son:
ax.scatter(84.92, -69.77, transform=ax.get_transform('fk5'), s=300, edgecolor='white', facecolor='none')
ax.coords[0].set_ticklabel_position('l')
#ax.coords[0].grid(color='white', ls='dotted')
ax.set_ylabel('RA')
ax.coords[1].set_ticklabel_position('b')
#ax.coords[1].grid(color='white', ls='dotted')
ax.set_xlabel('Dec');

Contornos¶
El trazado de imágenes como mapas de bits o contornos debe hacerse mediante los métodos habituales de matplotlib como imshow() o contour(). Por ejemplo, continuando con el ejemplo de inicializar ejes con WCS, se puede hacer:
[34]:
import numpy as np
fig = plt.figure(figsize=(8, 8))
ax = fig.add_subplot(1, 1, 1, projection=wcs)
im = ax.imshow(g, vmin=np.min(g), vmax=np.median(g)*2, origin='lower')
# Levels:
# Determina el número y las posiciones de las curvas de nivel / regiones.
# Si es un int n, utiliza MaxNLocator, que intenta elegir automáticamente no más de n+1 niveles de contorno "agradables" entre vmin y vmax.
# Si es un array, dibuja las curvas de nivel en los niveles especificados. Los valores deben estar en orden creciente.
ax.contour(g, transform=ax.get_transform(wcs), levels= [1690,1700], colors='white')
ax.coords[0].set_ticklabel_position('l')
#ax.coords[0].grid(color='white', ls='dotted')
ax.set_ylabel('RA')
ax.coords[1].set_ticklabel_position('b')
#ax.coords[1].grid(color='white', ls='dotted')
ax.set_xlabel('Dec');

Aplicación de WCS: Alineado de imágenes¶
Como ejercicio podemos alinear estrellas utilizando las coordenadas WCS de nuestras imagenes H-alpha, SII y OIII (que no conseguíamos alinear correctamente antes).
Realizaremos una función en el que podamos introducir el directorio o los valores de las propias imágenes para que me devuelva las imágenes alineadas.
[35]:
import numpy as np
import matplotlib.pyplot as plt
from astropy.io import fits
from astropy.wcs import WCS
import glob
from astropy import units as u
from astropy.coordinates import SkyCoord
import math
from scipy.ndimage.interpolation import rotate
def shift_image(X, dx, dy):
''''
X: imagen que queremos desplazar
dx: cantidad de píxeles de desplazamiento en el eje x
dy: cantidad de píxeles de desplazamiento en el eje x
return: imagen desplazada en un ndarray
'''
X = np.roll(X, dy, axis=0)
X = np.roll(X, dx, axis=1)
if dy>0:
X[:dy, :] = 0
elif dy<0:
X[dy:, :] = 0
if dx>0:
X[:, :dx] = 0
elif dx<0:
X[:, dx:] = 0
return X
def aling_wcs(directorio):
''''
directorio: donde se encuenrtan las imagenes que queremos alinear, importante solo tener las que queremos alinear.
return: ndarray con las imagenes alineadas.
'''
imagenes_header = []
imagenes_data = []
wcs = []
lista_imagenes = sorted(glob.glob(f"{directorio}*"))
for imagenes in lista_imagenes:
hdu = fits.open(imagenes)
imagenes_header.append(hdu[0].header)
imagenes_data.append(hdu[0].data)
wcs.append(WCS(header=hdu[0].header))
hdu.close()
ra_centro_ref = imagenes_header[0]['CRVAL1']*u.degree
dec_centro_ref = imagenes_header[0]['CRVAL2']*u.degree
centro_imagen_ref = SkyCoord(ra_centro_ref ,dec_centro_ref , frame='icrs')
x_centro = []
y_centro = []
for imagen in range(len(lista_imagenes)):
x_centro.append(wcs[imagen].world_to_pixel(centro_imagen_ref)[0])
y_centro.append(wcs[imagen].world_to_pixel(centro_imagen_ref)[1])
dx = []
dy = []
for imagen in range(len(lista_imagenes)):
dx.append(round(x_centro[0] - x_centro[imagen]))
dy.append(round(y_centro[0] - y_centro[imagen]))
imagenes_desplazadas = []
for imagen in range(len(lista_imagenes)):
imagenes_desplazadas.append(shift_image(imagenes_data[imagen], dx[imagen], dy[imagen]))
sky = wcs[0].pixel_to_world(0, 0)
x_cero = []
y_cero = []
for imagen in range(len(lista_imagenes)):
x_cero.append(wcs[imagen].world_to_pixel(sky)[0])
y_cero.append(wcs[imagen].world_to_pixel(sky)[1])
angulo = [] # defino una lista vacia en la que voy a tener en cuenta el angulo de rotacion que hay que aplicar a cada imagen
for i in range(len(lista_imagenes)):
#angulo.append(math.degrees(math.atan2(y[i][1] - y[i][0], x[i][1] - x[i][0]))) # calculo el angulo entre dos puntos de la misma imagen
angulo.append(round(math.degrees(math.atan2(y_cero[i] - y_centro[i], x_cero[i] - x_centro[i])))) # calculo el angulo entre dos puntos de la misma imagen
imagenes_derotadas = [imagenes_desplazadas[0], ] # aquí uso la funcion rotate(imagen, angulo_de_rotacion) de la biblioteca scipy
for i in range(1,len(lista_imagenes)):
imagenes_derotadas.append(rotate(imagenes_desplazadas[i], angle=angulo[0]-angulo[i]))
print(f"La imagen {i} está rotada {angulo[0]-angulo[i]} grados")
return imagenes_desplazadas
[36]:
directorio = 'salidas/salidaCalibracion/sho/'
h, o, s = aling_wcs(directorio)
WARNING: FITSFixedWarning: RADECSYS= 'FK5 ' / Equatorial coordinate system
the RADECSYS keyword is deprecated, use RADESYSa. [astropy.wcs.wcs]
WARNING: FITSFixedWarning: 'datfix' made the change 'Set MJD-OBS to 58887.129340 from DATE-OBS'. [astropy.wcs.wcs]
WARNING: FITSFixedWarning: 'datfix' made the change 'Set MJD-OBS to 58887.162245 from DATE-OBS'. [astropy.wcs.wcs]
WARNING: FITSFixedWarning: 'datfix' made the change 'Set MJD-OBS to 58888.090220 from DATE-OBS'. [astropy.wcs.wcs]
La imagen 1 está rotada 0 grados
La imagen 2 está rotada 0 grados
[37]:
rgb_default = make_lupton_rgb(s, h, o,Q=1,stretch=3000,filename="salidas/salidaCalibracion/shoTarantula.jpg")
[38]:
plt.figure(figsize=(8, 8))
plt.imshow(rgb_default, origin='lower', norm=norm)
plt.show()

[39]:
plt.figure(figsize=(8, 8))
plt.imshow(rgb_default[2000:2500,2000:2500], origin='lower', norm=norm)
plt.show()
