F: Tratamiento de una imagen científica (Ha-R)¶

Vamos a estudiar las regiones HII de la galaxia NGC6118. Para ello tendremos que preparar dos imágenes con diferentes filtros, Ha y R ya que sabemos que el filtro Ha es un filtro estrecho centrado en la banda 6607A y el filtro R, aunque está centrado en esas longitudes de onda, es más amplio.

Por lo tanto, lo que haremos es realizar una fotometría de las estrellas en la imagen Ha ya que tiene menos estrellas que la imagen R y a partir de la imagen R podemos añadir alguna estrella que no esté en Ha.

Una vez realizada la fotometría, debemos graficar los flujos de los dos filtros y trazar la recta de ajuste. Así conseguiremos realizar una estimación de la diferencia de flujo debido a los filtros.

Localizar estas regiones es importante en astronomía porque nos pueden ayudar a estudiar la velocidad radial de las galaxias como proponen Kam, Z. S et. al.

Abriendo las imágenes¶

[1]:

import matplotlib.pyplot as plt
import numpy as np
from astropy.io import fits
import os
import pandas as pd
import matplotlib.patches as patches
import scipy

from photutils import aperture_photometry
from photutils import CircularAperture
from astropy.stats import sigma_clipped_stats
from photutils import DAOStarFinder
from photutils import make_source_mask

from mpl_toolkits.mplot3d import Axes3D
from photutils.isophote import EllipseGeometry

from sklearn.linear_model import LinearRegression
from sklearn import linear_model
from sklearn.metrics import mean_squared_error, r2_score

[2]:

ha=fits.open("imagenes/regionHII/ha.fit")[0].data[400:-400,400:-400]
r=fits.open("imagenes/regionHII/r.fit")[0].data[400:-400,400:-400]

Detectando estrellas en `Ha`¶

DAOStarFinder Stetson 1987; PASP 99, 191 busca en las imágenes los máximos de densidad en el flujo.

[3]:

mean, median, std = sigma_clipped_stats(ha, sigma=3.0) # definimos una mediana con sigma_clipped_stats
daofind = DAOStarFinder(fwhm=3.0, threshold=80.*std)   # detectamos las fuentes con DAOStarFinder
mask = np.zeros(ha.shape, dtype=bool)                  # Generamos una mascara para qutar el centro de la imagen
mask[200:1000, 200:1000] = True
sources = daofind(ha - median, mask=mask)              # detectamos las fuentes que esten por encima de la mediana
for col in sources.colnames:
    sources[col].info.format = '%.8g'                  # formateo de la tabla
print(sources)

 id xcentroid ycentroid sharpness  ... sky    peak       flux       mag
--- --------- --------- ---------- ... --- ---------- --------- ------------
  1 349.08407  23.06115 0.45760264 ...   0 0.28782383  1.120405  -0.12343756
  2 1252.3425 111.83957 0.49992619 ...   0  1.7884092 7.9329739   -2.2485901
  3 100.84967 141.65812  0.4519161 ...   0   2.009676 7.3235307   -2.1618013
  4 139.75055 154.01524 0.49915704 ...   0 0.39054054 1.4219631  -0.38222081
  5  398.0879 182.65515 0.47621736 ...   0 0.36278591 1.5117347  -0.44868897
  6 1242.7372 644.93147 0.41871981 ...   0 0.51455635 2.4777501  -0.98514374
  7 1050.4904 648.32583 0.51884046 ...   0 0.64771599 2.9557924   -1.1766848
  8 565.11216 1021.5083  0.4412611 ...   0 0.30307603 1.3398254  -0.31762051
  9 299.00671  1132.516 0.46488908 ...   0 0.49880373 2.1088767  -0.81012797
 10 327.52825 1144.4042 0.42840471 ...   0  11.307342  47.39386   -4.1893052
 11 245.92845 1271.7488 0.45522224 ...   0 0.41422138 1.7048297   -0.5792025
 12 660.31653 1274.4656 0.49179181 ...   0 0.25255319 1.0765691 -0.080104756

[4]:

plt.figure("Stars in Ha", figsize=[10, 10])
positions = np.transpose((sources['xcentroid'], sources['ycentroid']))
apertures = CircularAperture(positions, r=10.)
plt.imshow(ha,vmin=0, vmax=0.01, origin='lower')
apertures.plot(color='red', lw=1.5, alpha=0.5)
plt.show()

Una vez detectadas las fuentes calculamos la apertura circular en un radio de 20 píxeles:

[5]:

aperture = CircularAperture(positions, r=20.)

Y calculamos la fotometría de dicha apertura:

[6]:

phot_table_Ha = aperture_photometry(ha, aperture)
phot_table_Ha

[6]:

QTable length=12

id	xcenter	ycenter	aperture_sum
	pix	pix
int64	float64	float64	float64
1	349.0840718721037	23.06115023990617	5.9707853144109375
2	1252.3425282476803	111.8395660192342	31.12198779628524
3	100.84967175575383	141.65812290255334	46.177683387858465
4	139.75055253162196	154.01523501983976	9.187212283913759
5	398.0878982067919	182.65514850657365	7.112305744900143
6	1242.7372495712386	644.9314689138399	8.795779939807034
7	1050.4903937456747	648.3258263525412	10.492986704029342
8	565.1121596416924	1021.5082530499211	5.3790705228001165
9	299.00671132484865	1132.5160282322252	11.273667917231116
10	327.52824953169124	1144.4041834299107	227.57507170675046
11	245.92844626442664	1271.7487790690082	8.20190432025236
12	660.3165326153387	1274.4656046219322	4.054421322970487

[7]:

plt.figure("Stars in R", figsize=[10, 10])
positions = np.transpose((sources['xcentroid'], sources['ycentroid']))
apertures = CircularAperture(positions, r=10.)
plt.imshow(r, vmin=np.nanmin(r), vmax=np.nanmedian(r)*800, origin='lower')
apertures.plot(color='red', lw=1.5, alpha=0.5)
plt.show()

[8]:

phot_table_R = aperture_photometry(r, aperture)
phot_table_R

[8]:

QTable length=12

id	xcenter	ycenter	aperture_sum
	pix	pix
int64	float64	float64	float64
1	349.0840718721037	23.06115023990617	198.1431176575303
2	1252.3425282476803	111.8395660192342	1236.7766704090466
3	100.84967175575383	141.65812290255334	1690.1940084358525
4	139.75055253162196	154.01523501983976	307.37253223122707
5	398.0878982067919	182.65514850657365	231.46341415609555
6	1242.7372495712386	644.9314689138399	334.2297095809117
7	1050.4903937456747	648.3258263525412	360.05377588415286
8	565.1121596416924	1021.5082530499211	197.14452375154906
9	299.00671132484865	1132.5160282322252	451.45046283292936
10	327.52824953169124	1144.4041834299107	8390.575172524223
11	245.92844626442664	1271.7487790690082	296.45947593985693
12	660.3165326153387	1274.4656046219322	154.4934309550923

Ha vs R¶

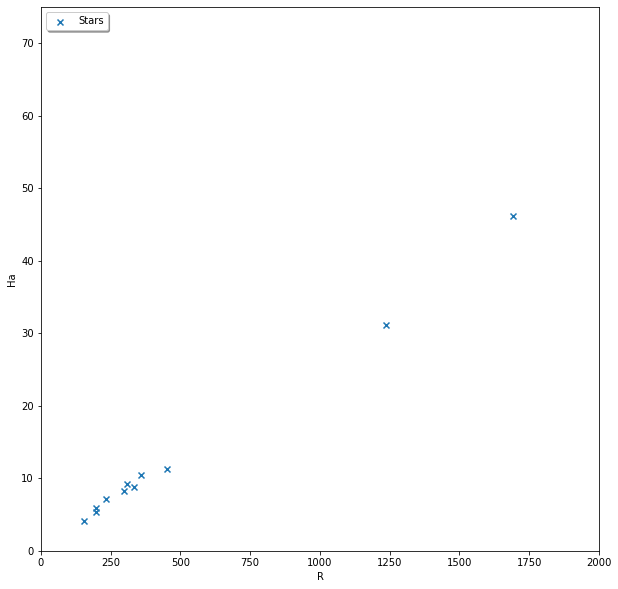
Comparamos el flujo de el filtro de H-alpha y el del canal rojo:

[9]:

plt.figure("Ha vs R", figsize=[10, 10])
plt.scatter(phot_table_R['aperture_sum'],phot_table_Ha['aperture_sum'] , marker='x', alpha=1, label='Stars')
plt.xlim(0, 2000)
plt.ylim(0, 75)
plt.legend (loc='upper left', shadow=True, fontsize='medium')
plt.ylabel("Ha")
plt.xlabel("R")
plt.show()

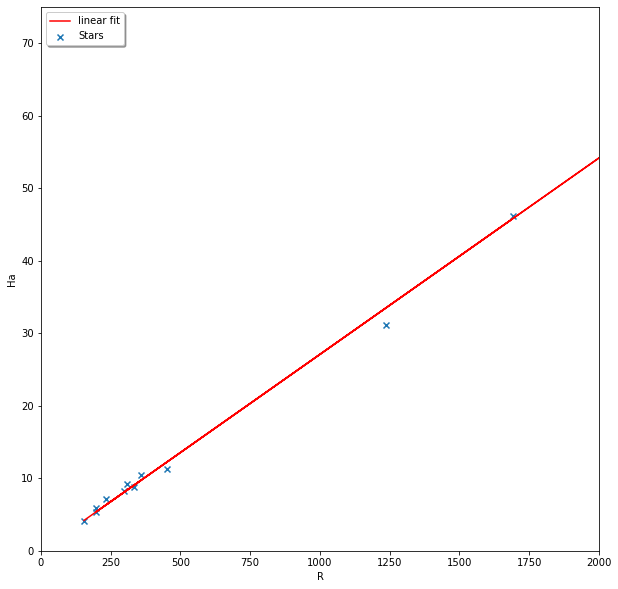
Ajuste lineal: \(Ha = aR+b\)¶

Realizamos un ajuste lineal para determinar la compensación de flujo:

[10]:

# y = ax + b
regresion_lineal = LinearRegression()

regresion_lineal.fit(np.asarray(phot_table_R['aperture_sum']).reshape(-1,1), np.asarray(phot_table_Ha['aperture_sum']))
a = regresion_lineal.coef_
b = regresion_lineal.intercept_
print('a = ' + str(a) + ', b = ' + str(b))

a = [0.02709269], b = 0.012804110295842719

\(R^2\)¶

[11]:

r2 = regresion_lineal.score(np.asarray(phot_table_R['aperture_sum']).reshape(-1,1), np.asarray(phot_table_Ha['aperture_sum']))
print('Coeficiente de determinacion R2 = ' + str(r2))

Coeficiente de determinacion R2 = 0.999787706607886

Graficando Ha vs R y su ajuste lineal¶

[12]:

plt.figure("Ha vs R", figsize=[10, 10])
y_ajuste = phot_table_R['aperture_sum']*a + b
# Dibujamos la recta de ajuste
plt.plot(phot_table_R['aperture_sum'], y_ajuste, 'r-', label ='linear fit')
plt.scatter(phot_table_R['aperture_sum'],phot_table_Ha['aperture_sum'] , marker='x', alpha=1, label='Stars')
plt.xlim(0, 2000)
plt.ylim(0, 75)
plt.legend (loc='upper left', shadow=True, fontsize='medium')
plt.ylabel("Ha")
plt.xlabel("R")
plt.show()

Multiplicando la imagen del filtro R por a¶

[13]:

r_scale = r * a

Sustrayendo la imagen R de la imagen Ha¶

[14]:

Ha_R = ha - r_scale

[15]:

Ha_R

[15]:

array([[ 5.87614958e-04, -2.22705754e-03, -6.33193890e-05, ...,
        -1.95511944e-03, -2.19005413e-03, -1.07355891e-03],
       [ 1.44865865e-03,  1.68791693e-03, -2.92267763e-03, ...,
        -5.02979401e-03, -1.32460991e-04,  2.46133466e-03],
       [-1.45900960e-03, -1.07090869e-03,  6.85737659e-04, ...,
        -1.65304801e-03, -2.56703439e-03,  3.42935420e-04],
       ...,
       [-2.10557561e-03,  3.17371688e-03, -1.01978432e-03, ...,
        -8.15871924e-03, -9.66137502e-03, -6.33899882e-03],
       [-3.50515216e-04, -1.37433936e-04,  3.51346817e-03, ...,
        -9.14807545e-03, -4.38527888e-03, -9.54893225e-03],
       [-1.00476876e-03,  1.81116940e-03,  1.69438158e-03, ...,
        -5.03344479e-03, -8.53135309e-03, -6.68820593e-03]])

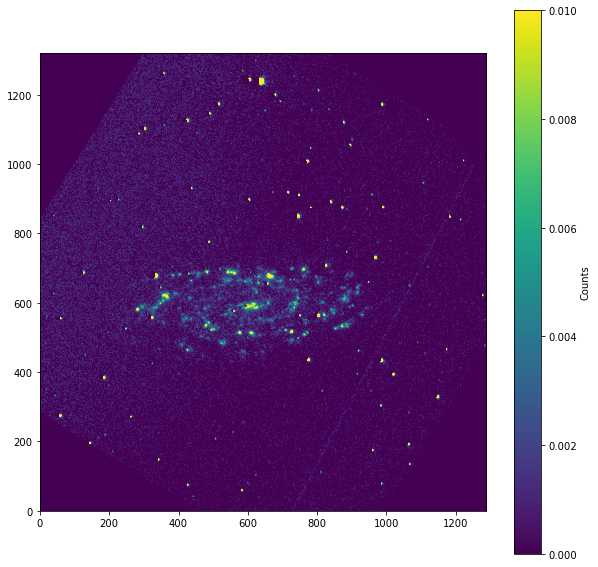
Graficando Ha-R¶

[16]:

plt.figure("Ha-R", figsize=[10, 10])
plt.imshow(Ha_R, vmin=0, vmax=0.01, origin='lower')
plt.colorbar(label='Counts')
plt.show()

Guardando Ha-R¶

[17]:

hdu_Ha = fits.PrimaryHDU(Ha_R.astype(np.float32))
hdu_Ha.writeto('salidas/Ha_R.fit', overwrite=True)

Buscando las regiones HII en nuestra imagen¶

La galaxia no está de frente: tiene un ángulo de inclinación que debemos corregir. Para ello primero rotaremos la imagen y luego aplicaremos una transformación a los ejes (tenemos una galaxia con forma de elipse y sabemos que las galaxias espirales son circulares).

Utilizaremos el paquete ndimage de SciPy.

Rotando la imagen¶

[18]:

from scipy import ndimage, misc

[19]:

#geometry = EllipseGeometry(x0=658, y0=682, sma=20, eps=0.5,pa=20.*np.pi/180.)

[20]:

Ha_R_rotate = scipy.ndimage.rotate(Ha_R, 32, reshape=False, output=None, order=3, mode='constant', cval=0.0, prefilter=True)

[21]:

plt.figure("master_Ha-R scale", figsize=[10, 10])
plt.imshow(Ha_R_rotate, vmin=0, vmax=0.01, origin='lower')
plt.colorbar(label='Counts')
plt.show()

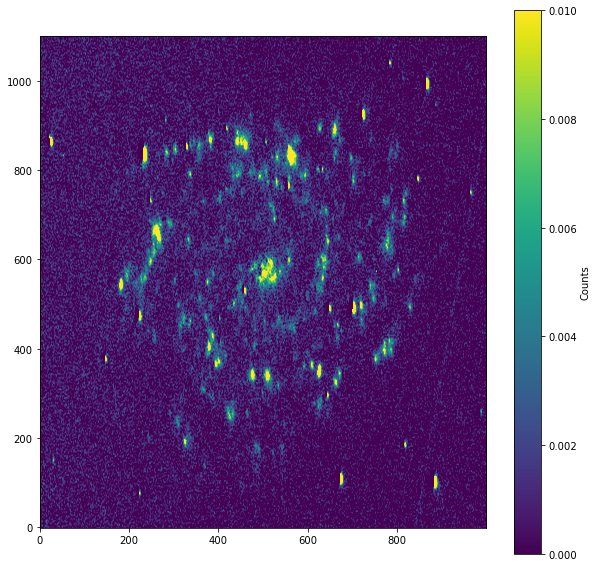
Transformando la galaxia eliptica en galaxia circular¶

[22]:

transform = ndimage.zoom(Ha_R_rotate, [3, 1])

[23]:

plt.figure("master_Ha-R scale", figsize=[10, 10])
plt.imshow(transform[1200:2300,100:1100], vmin=0, vmax=0.01, origin='lower')
plt.colorbar(label='Counts')
plt.show()

Buscando las regiones de Ha¶

Ahora vamos a buscar las regiones HII de nuestra galaxia.

Para ello usaremos la herramienta que habíamos utilizado anteriormente para la detección de estrellas DAOStarFinder.

Encontramos 113 fuentes de HII aunque tenemos que tener cuidado con los parámetros que elegimos ya que se nos puede colar estructura que no queremos o estrellas. Para evitar esto, es bueno utilizar máscaras para evitar regiones fuera de la galaxia.

[24]:

mean_H, median_H, std_H = sigma_clipped_stats(transform[1200:2300,100:1100], sigma=0.8)
daofind_H = DAOStarFinder(fwhm=10, threshold=150*std_H, sharplo = 0., sharphi=200, roundlo=0.01, roundhi=500)

star_mask = np.zeros(transform[1200:2300,100:1100].shape, dtype=bool)

star_mask[:200,0:250] = True

star_mask[:,0:125] = True
star_mask[879:,:] = True
star_mask[:,835:] = True
star_mask[0:226,674:] = True
star_mask[820:,0:247] = True

sources_H = daofind_H(transform[1200:2300,100:1100] - median_H, mask=star_mask)
for col in sources_H.colnames:
    sources_H[col].info.format = '%.8g'  # for consistent table output
print(sources_H)

 id xcentroid ycentroid  sharpness   ... sky     peak        flux       mag
--- --------- --------- ------------ ... --- ------------ --------- ------------
  1 673.34791 108.28638   0.58854268 ...   0   0.28304639 89.848598   -4.8837783
  2 462.70304 258.05397   0.54279086 ...   0 0.0046983214 1.2345386  -0.22876165
  3 624.21743 274.30205   0.60176744 ...   0 0.0064568319 1.0659275 -0.069319183
  4 613.55167  278.6011   0.43907255 ...   0  0.003923736 1.0261012 -0.027975484
  5 643.86824 296.38696   0.63987169 ...   0  0.014474816 3.5996975    -1.390665
  6 632.08163 300.79437   0.31789377 ...   0 0.0013197177 1.1323417  -0.13494377
  7 532.54896  318.6302   0.81185107 ...   0 0.0067532225 1.1485891  -0.15041173
  8 508.69781 339.63691   0.57408677 ...   0   0.02770378 4.9978188   -1.7469513
  9 669.65575 345.57069   0.58891515 ...   0  0.011462141 2.5940775   -1.0349574
 10  624.1418 349.24394   0.64078115 ...   0  0.050128334 10.201395   -2.5216489
...       ...       ...          ... ... ...          ...       ...          ...
101 381.30952 853.14788   0.78079617 ...   0 0.0070736353 1.1861123   -0.1853145
102 328.84897 851.59042   0.34346848 ...   0  0.016070412 7.2664881   -2.1533114
103 355.89246 855.33059   0.34203403 ...   0 0.0067478149 1.6131511  -0.51918761
104 458.67073 856.32579   0.43982402 ...   0  0.019264253 3.3750725   -1.3207078
105 450.24039 862.20012    0.8537384 ...   0  0.015236503 1.4662118  -0.41549181
106 506.03888 862.30651   0.57528107 ...   0 0.0091484959 3.1322564   -1.2396433
107 440.66565 864.09099   0.56855257 ...   0  0.017679877 3.0222884   -1.2008398
108 670.41467 867.16907   0.55048246 ...   0  0.005257102 1.1646337  -0.16547335
109 739.44706 868.26639   0.21047435 ...   0 0.0019689948 1.0423443 -0.045028041
110 380.66416 868.77978   0.69323155 ...   0  0.027843254 5.4233501   -1.8356691
111 656.68877 873.95501 0.0093337942 ...   0 0.0033410237  1.060428 -0.063703009
Length = 111 rows

[25]:

plt.figure("HII regions", figsize=[10, 10])
positions_H = np.transpose((sources_H['xcentroid'], sources_H['ycentroid']))
apertures_H = CircularAperture(positions_H, r=10.)
plt.imshow(transform[1200:2300,100:1100], vmin=0, vmax=0.01, origin='lower')
plt.colorbar(label='Counts')
apertures_H.plot(color='red', lw=1.5, alpha=0.6)
plt.show()

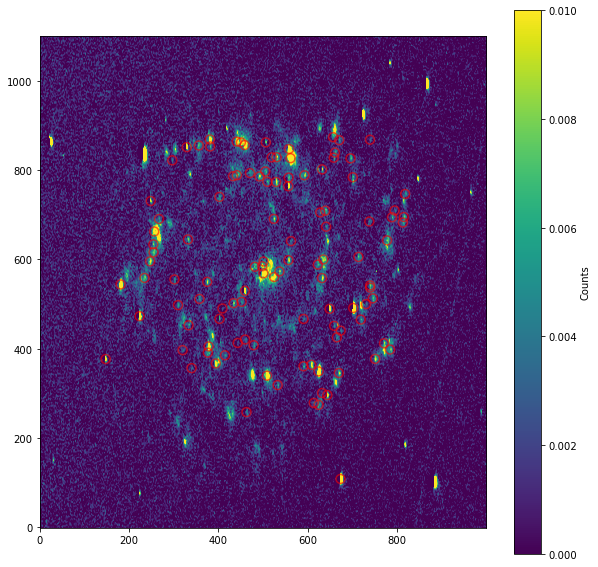
Trazando todas las fuentes de HII encontradas en la galaxia¶

Ahora vamos a representar estas regiones en 2D y 3D.

Las posiciones que nos ha ofrecido daofind son respecto a la imagen, por lo tanto vamos a recalcular todas las posiciones respecto al centro de la galaxia.

En el gráfico hemos rescalado el flujo que nos da la barra de color para tener un mayor contraste (aplicando el logaritmo a los datos).

También hemos reescalado el tamaño de las regiones HII, hemos tomado el pico de la distribución medido por daofind y lo hemos multiplicado por 5000.

Para hacer la representación en 3D hemos supuesto que la anchura de la galaxia es muy pequeña comparada con el tamaño de los brazos.

Centro de la galaxia¶

[26]:

H_x_center = 0 #500
H_y_center = 0 #580

Centrando los valores del eje `x`¶

[27]:

H_x = sources_H['xcentroid'] -500

Centrando los valores del eje `y`¶

[28]:

H_y = sources_H['ycentroid'] -580

Gráfico de dispersión (Sccater plot)¶

[29]:

plt.figure('Distribution of HII regions in 2D', figsize=[10, 10])
plt.subplot(111, aspect = 'equal')
plt.scatter(H_x, H_y, vmin=np.log10(np.min(sources_H['flux']))/2,
            vmax=np.log10(np.max(sources_H['flux'])), c=np.log10(sources_H['flux']),
            s=5000*sources_H['peak'], alpha=.6)

plt.colorbar(label='Flux')
plt.plot(H_x_center, H_y_center, 'r' ,marker='+', alpha=1, markersize=20)

[29]:

[<matplotlib.lines.Line2D at 0x7f894c5c0bb0>]

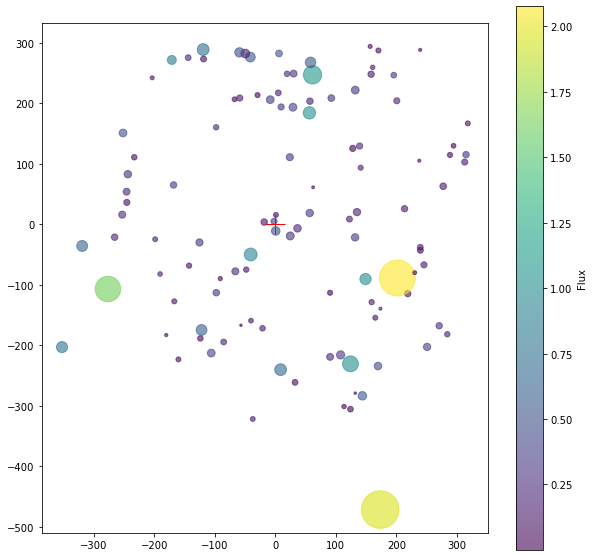
[30]:

fig = plt.figure('Distribution of HII regions in 3D', figsize=[10, 10])
ax = Axes3D(fig, auto_add_to_figure=False)
fig.add_axes(ax)
ax.scatter(H_x, H_y, 1 , vmin=np.log10(np.min(sources_H['flux'])),
           vmax=np.log10(np.max(sources_H['flux'])),
           c=np.log10(sources_H['flux']),
           s=5000*sources_H['peak'])

ax.set_xlabel('X position')
ax.set_ylabel('Y position')
ax.set_zlabel('Z position')
plt.plot(H_x_center, H_y_center,1, 'r' ,marker='+', alpha=1, markersize=20)

plt.show()

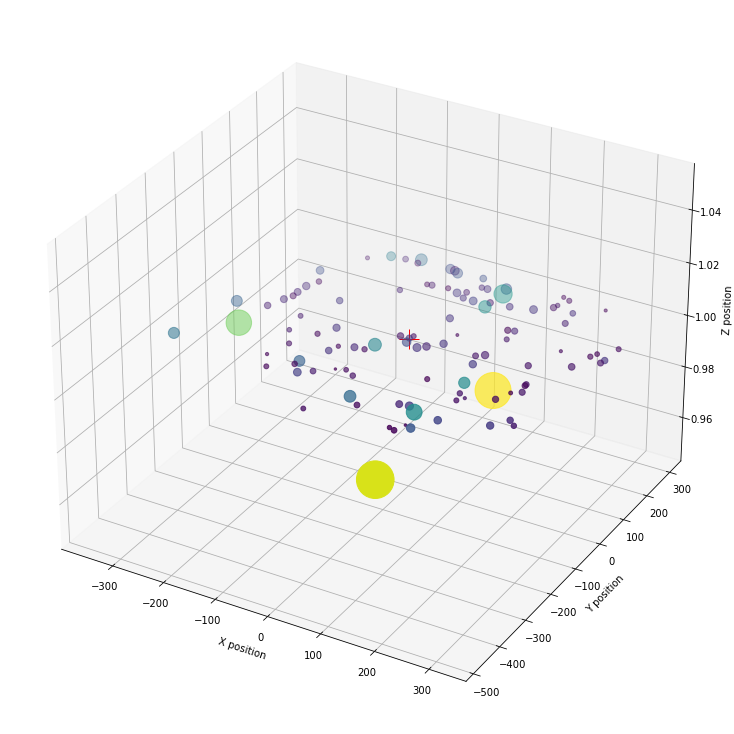
Exportación de datos para una simulación de la rotación de la galaxia.¶

Podemos exportar los datos para poder hacer una simulación muy básica de la rotación de la galaxia.

[31]:

rotate = ({"x":H_x, "y":H_y, "flux":sources_H['flux'], "peak":sources_H['peak']})

[32]:

table_df = pd.DataFrame(rotate)
table_df.to_csv('salidas/table_rotation.csv')